Key Recovery SDCTF 2022

Challenge Files

This challenge involved fixing an OpenSSH Private Key. Let’s start by analysing a dummy, non-corrupted key:

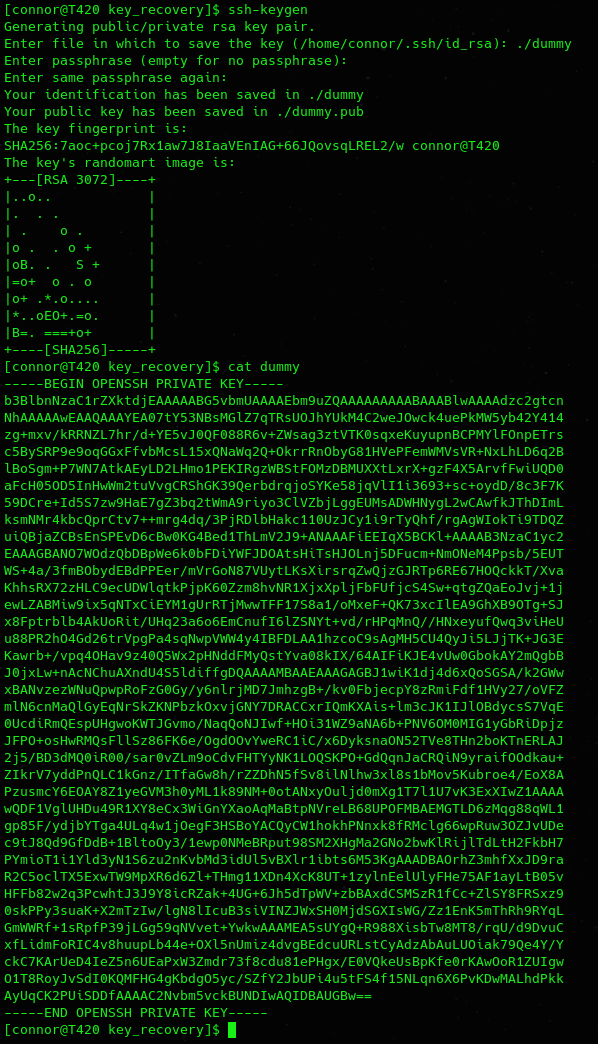
We can generate a public pem key from this:

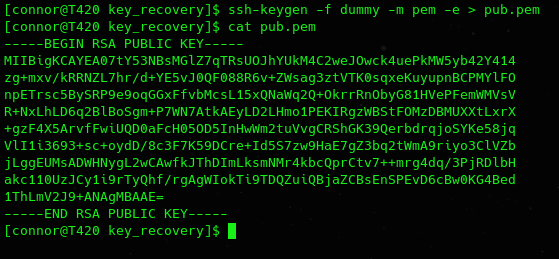
Using similar technique in Information Paradox from Space Heroes CTF 2022
we can get n and e from the public key:

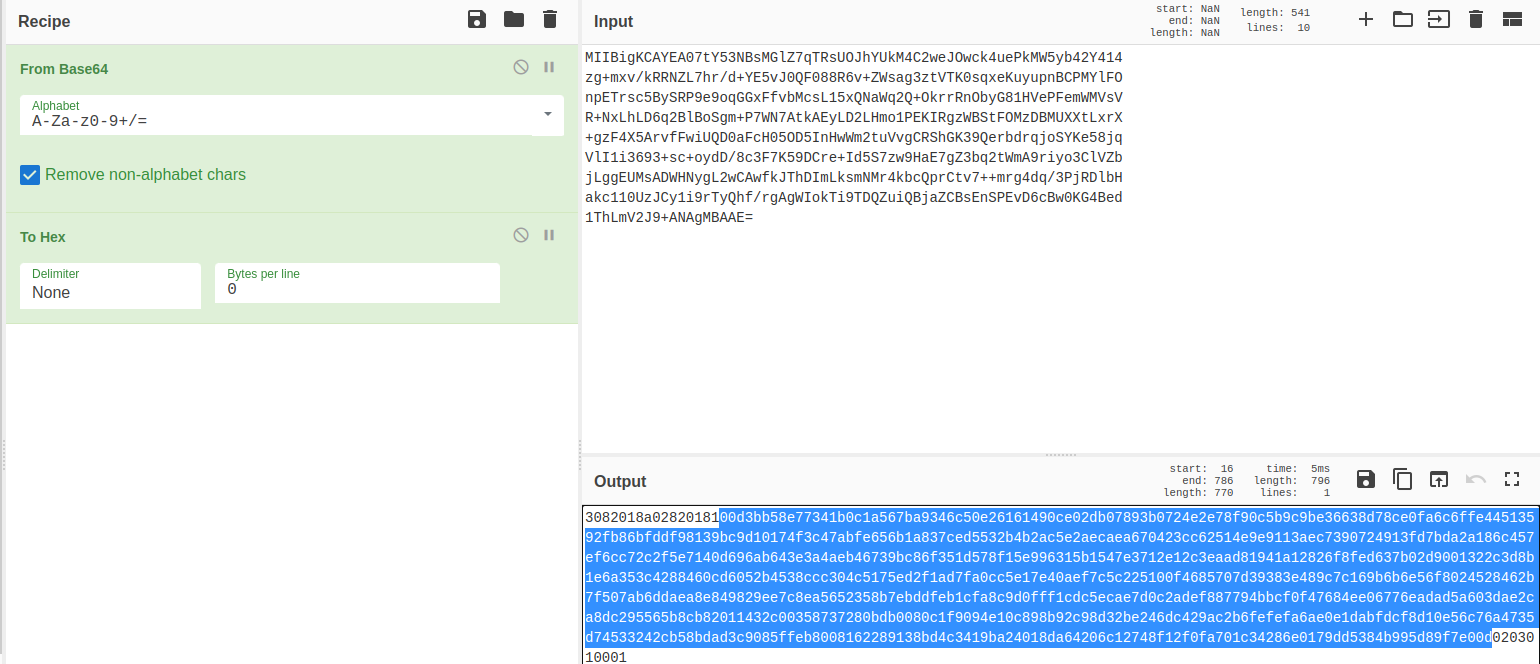
Now let’s analyse the openssh private key. I’ve highlighted values in yellow, and headers in green. We see n and e appear twice:

From this blog https://dnaeon.github.io/openssh-private-key-binary-format/ I found this table useful:

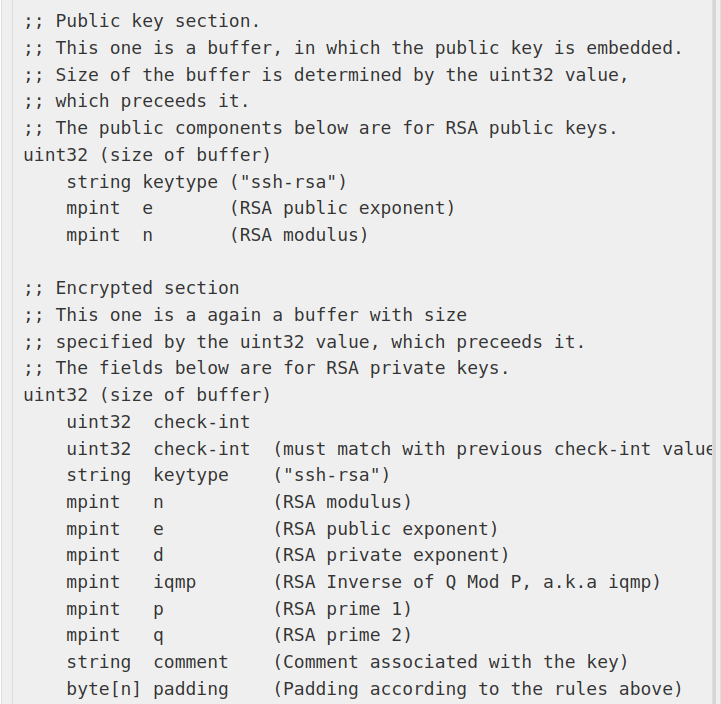
So next value is d (in blue):

This is enough to create our own PEM private key:

from Crypto.PublicKey import RSA
from Crypto.Util.number import *
import random
from math import gcd

e = 0x10001
n = 0x00d3bb58e77341b0c1a567ba9346c50e26161490ce02db07893b0724e2e78f90c5b9c9be36638d78ce0fa6c6ffe44513592fb86bfddf98139bc9d10174f3c47abfe656b1a837ced5532b4b2ac5e2aecaea670423cc62514e9e9113aec7390724913fd7bda2a186c457ef6cc72c2f5e7140d696ab643e3a4aeb46739bc86f351d578f15e996315b1547e3712e12c3eaad81941a12826f8fed637b02d9001322c3d8b1e6a353c4288460cd6052b4538ccc304c5175ed2f1ad7fa0cc5e17e40aef7c5c225100f4685707d39383e489c7c169b6b6e56f8024528462b7f507ab6ddaea8e849829ee7c8ea5652358b7ebddfeb1cfa8c9d0fff1cdc5ecae7d0c2adef887794bbcf0f47684ee06776eadad5a603dae2ca8dc295565b8cb82011432c00358737280bdb0080c1f9094e10c898b92c98d32be246dc429ac2b6fefefa6ae0e1dabfdcf8d10e56c76a4735d74533242cb58bdad3c9085ffeb8008162289138bd4c3419ba24018da64206c12748f12f0fa701c34286e0179dd5384b995d89f7e00d
d = 0x181275c222b5763e1deb1428486480fe4d865b0c4100dbf37b358db90a70a51a05cc6d06cbfcba9e5ae3303ec99a1ce007efe4bf415b8de72963ccd19a215d7f51d5cb6effa151599a537a72731a4251b212a36b4a464a34f6f390ec6f8c6358ec3440082c6b21098a5c08acfa59b77092b520994e05dc9cb12ed5a84d1471d89199012ca541e0c282964c91af9a8fcd6aa4283492307fe1ce8b7d5667d68d03a6fe3cd57a38cd0c206d7219b4620e98f32453cefa8b07c11310b059654b3f3a14ae9efce81d38ebd8c1e442d620bfc7a0f292c9da38de764d57bc4c79f66e82939c444b009da3e7f043ddd310d22474d3fb1aaf4bd92e6f6809dbc51d363234ad4b39048a3cef86750aa725a09142237dcab6a27ce39d91abbe64892b57bc9d74f9d02c2d641a7cff2137da1b0f21feb6590e13797d2bfc8a5365870df197cb356cca2fe4ab9bae87b8fc4a17f003f3bac99c63a10e018f19d7278654cde1d3230bd64f3d34cfb4a2d00dc723ae9637749978354fb97553bbcadc4c57230675

#https://gist.github.com/ddddavidee/b34c2b67757a54ce75cb
def outputPrimes(a, n):
	p = gcd(a, n)
	q = int(n // p)
	if p > q:
		p, q = q, p
	return p,q

def RecoverPrimeFactors(n, e, d):
        k = d * e - 1
        if k % 2 == 1:
                failFunction()
                return 0, 0
        else:
                t = 0
                r = k
                while(r % 2 == 0):
                        r = int(r // 2)
                        t += 1
                for i in range(1, 101):
                        g = random.randint(0, n) 
                        y = pow(g, r, n)
                        if y == 1 or y == n - 1:
                                continue
                        else:
                                for j in range(1, t): 
                                        x = pow(y, 2, n)
                                        if x == 1:
                                                p, q = outputPrimes(y - 1, n)
                                                return p, q
                                        elif x == n - 1:
                                                continue
                                        y = x
                                        x = pow(y, 2, n)
                                        if  x == 1:
                                                p, q = outputPrimes(y - 1, n)
                                                return p, q

p, q = RecoverPrimeFactors(n, e, d)

#print("n:", hex(n))
#print("e:", hex(e))
#print("d:", hex(d))
#print("p:", hex(p))
#print("q:", hex(q))

assert pow(e, -1, (p-1)*(q-1)) == d
assert isPrime(p)
assert isPrime(q)
assert p*q == n

key = RSA.construct((n,e,d,q,p))
pem = key.export_key('PEM')
print(pem.decode())

And with this, we can ‘almost’ re-create the openssh private key:

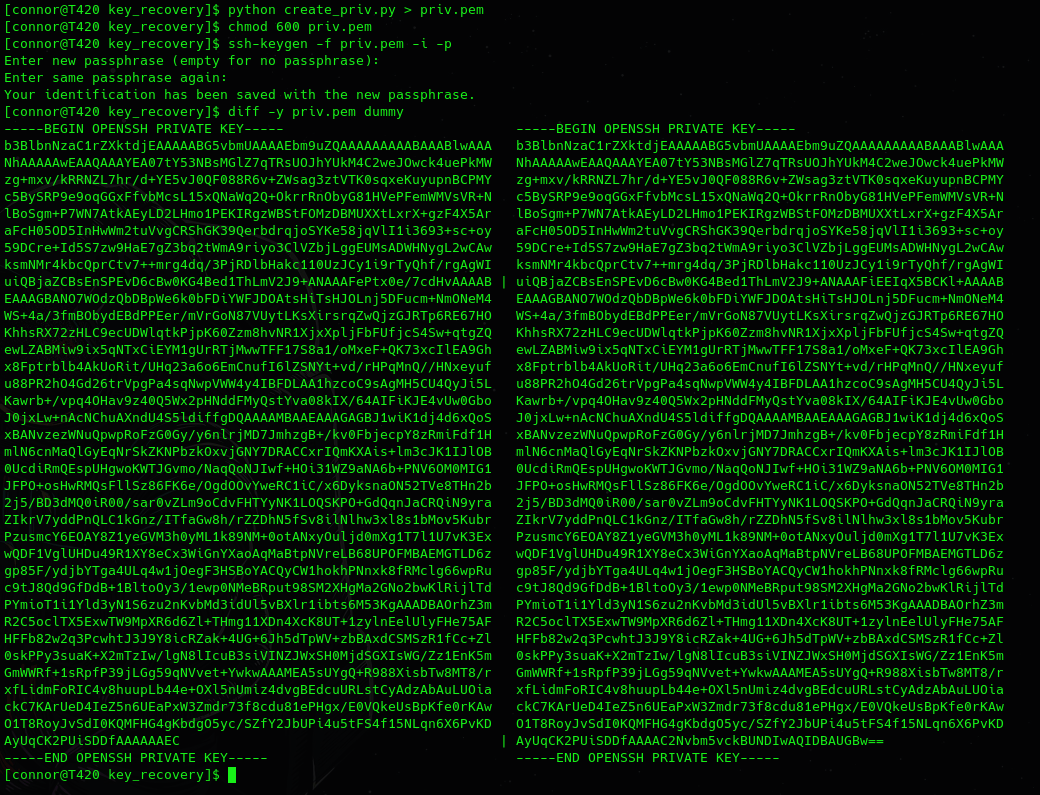
Two sections are different, the check-ints and the comment at bottom.
The check-ints are random, and my original key had the comment ‘connor@T420’ where the
re-created key had no comment.

Now the process to fix the key in this challenge is the exact same process
(luckily the check-ints and comment were not corrupted, so I could just modify those).
Here is the final solution (the flag was the sha256 hash):

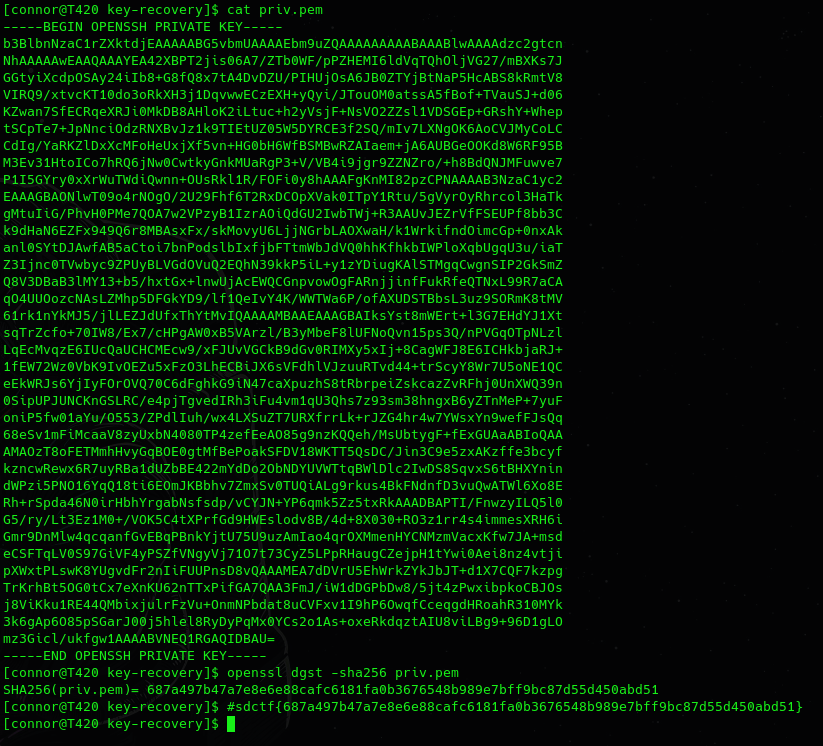
Update (2022): d must also be modified to use the Carmichael totient function rather than the Euler totient function.