Geometry Hash - Balsn CTF 2023

Challenge:

import secrets
from sympy import N, Float, Point, Triangle

#from secret import FLAG
FLAG = "testflag"

PRECISION = 1337

def main():
	import signal
	signal.alarm(20)

	levels = [
		lambda x: x.centroid,
		lambda x: x.circumcenter,
		lambda x: x.incenter,
	]
	try:
		for level in levels:
			challenge(level)
		print(FLAG)
	except:
		print("Wasted")

def challenge(hash_function):
	# raise an error if the user fails the challenge

	print("===== Challenge =====")
	A = RandomLine()
	B = RandomLine()
	C = RandomLine()

	# print parameters
	A.print()
	B.print()
	C.print()

	i, j, k = [secrets.randbits(32) for _ in range(3)]
	triangle = Triangle(A[i], B[j], C[k])
	hsh = hash_function(triangle)
	
	print(Float(hsh.x, PRECISION))
	print(Float(hsh.y, PRECISION))

	_i, _j, _k = map(int, input("> ").split(" "))
	assert (i, j, k) == (_i, _j, _k)
	print("Mission passed")

class RandomLine:
	def __init__(self):
		self.x = randFloat()
		self.y = randFloat()
		self.dx = randFloat()
		self.dy = randFloat()

	def __getitem__(self, i):
		return Point(self.x + self.dx * i, self.y + self.dy * i, evaluate=False)

	def print(self):
		print(self.x)
		print(self.y)
		print(self.dx)
		print(self.dy)

def randFloat():
	# return a random float between -1 and 1
	return -1 + 2 * Float(secrets.randbits(PRECISION), PRECISION) / (1 << PRECISION)

if __name__ == "__main__":
	main()

Solve:

	A = RandomLine()
	B = RandomLine()
	C = RandomLine()
	i, j, k = [secrets.randbits(32) for _ in range(3)]
	triangle = Triangle(A[i], B[j], C[k])

Note that the vertices of the triangles are unknown, given by:

	def __getitem__(self, i):
		return Point(self.x + self.dx * i, self.y + self.dy * i, evaluate=False)

So I’ll denote:

\[(x1, \ y1) = (Ax + Adx \cdot i, \ Ay + Ady \cdot i)\] \[(x2, \ y2) = (Bx + Bdx \cdot j, \ By + Bdy \cdot j)\] \[(x3, \ y3) = (Cx + Cdx \cdot k, \ Cy + Cdy \cdot k)\]

Part 1 - Centroid:

We have 2 equations with 3 relatively small unknowns (i, j, k):

\[\text{centroidX} = \frac{x1 + x2 + x3}{3} = \frac{Ax + Adx \cdot i + Bx + Bdx \cdot j + Cx + Cdx \cdot k}{3}\] \[\text{centroidY} = \frac{y1 + y2 + y3}{3} = \frac{Ay + Ady \cdot i + By + Bdy \cdot j + Cy + Cdy \cdot y}{3}\]

Now we can rewrite them for LLL:

\[i \begin{bmatrix}Adx \\ Ady \\ 1 \\ 0 \\ 0\end{bmatrix} + j \begin{bmatrix}Bdx \\ Bdy \\ 0 \\ 1 \\ 0\end{bmatrix} + k \begin{bmatrix}Cdx \\ Cdy \\ 0 \\ 0 \\ 1\end{bmatrix} + \begin{bmatrix}Ax+Bx+Cx-3\cdot\text{centroidX} \\ Ay+By+Cy-3\cdot\text{centroidY} \\ 0 \\ 0 \\ 0\end{bmatrix} = \begin{bmatrix}0 (\pm \text{precision error}) \\ 0 (\pm \text{precision error}) \\ i \\ j \\ k\end{bmatrix}\]

Demo:

def r():
    return randint(0, 2**1000)

Ax, Bx, Cx    = r(), r(), r()
Ay, By, Cy    = r(), r(), r()
Adx, Bdx, Cdx = r(), r(), r()
Ady, Bdy, Cdy = r(), r(), r()

i, j, k = [randint(0, 2**32) for _ in range(3)]
print(i, j, k)
centroidX = (Adx*i + Bdx*j + Cdx*k + Ax + Bx + Cx) // 3
centroidY = (Ady*i + Bdy*j + Cdy*k + Ay + By + Cy) // 3

M = Matrix([
    [                       Adx,                        Ady, 1, 0, 0],
    [                       Bdx,                        Bdy, 0, 1, 0],
    [                       Cdx,                        Cdy, 0, 0, 1],
    [Ax + Bx + Cx - 3*centroidX, Ay + By + Cy - 3*centroidY, 0, 0, 0],
])

print(M.LLL()[0])

from sympy import Float, Triangle, Point
import secrets

class RandomLine:
    def __init__(self):
        self.x = randFloat()
        self.y = randFloat()
        self.dx = randFloat()
        self.dy = randFloat()

    def __getitem__(self, i):
        return Point(self.x + self.dx * i, self.y + self.dy * i, evaluate=False)

    def get(self):
        return self.x, self.y, self.dx, self.dy

def randFloat():
    # return a random float between -1 and 1
    PRECISION = 1337
    return -1 + 2 * Float(secrets.randbits(PRECISION), PRECISION) / (1 << PRECISION)

A = RandomLine()
B = RandomLine()
C = RandomLine()
i, j, k = [randint(0, 2**32) for _ in range(3)]
print(i, j, k)
triangle = Triangle(A[i], B[j], C[k])

Ax, Ay, Adx, Ady = A.get()
Bx, By, Bdx, Bdy = B.get()
Cx, Cy, Cdx, Cdy = C.get()
centroidX, centroidY  = triangle.centroid

# resize
n = 10**1337
Ax, Ay, Adx, Ady = int(Ax*n), int(Ay*n), int(Adx*n), int(Ady*n)
Bx, By, Bdx, Bdy = int(Bx*n), int(By*n), int(Bdx*n), int(Bdy*n)
Cx, Cy, Cdx, Cdy = int(Cx*n), int(Cy*n), int(Cdx*n), int(Cdy*n)
centroidX, centroidY = int(centroidX*n), int(centroidY*n)

M = Matrix([
    [                       Adx,                        Ady, 1, 0, 0],
    [                       Bdx,                        Bdy, 0, 1, 0],
    [                       Cdx,                        Cdy, 0, 0, 1],
    [Ax + Bx + Cx - 3*centroidX, Ay + By + Cy - 3*centroidY, 0, 0, 0],
])

print(M.LLL()[0][-3:])

Part 2 - Circumcenter:

The distances of the circumcenter (ccX, ccY) from each vertex ((x1, y1), (x2, y2), (x3, y3)) of a triangle are equal.

\[\sqrt{(ccX - x1)^2 + (ccY - y1)^2} = \sqrt{(ccX - x2)^2 + (ccY - y2)^2} = \sqrt{(ccX - x3)^2 + (ccY - y3)^2}\]

We can make two equations:

\[0 = (ccX - x1)^2 + (ccY - y1)^2 - (ccX - x2)^2 - (ccY - y2)^2\] \[0 = (ccX - x1)^2 + (ccY - y1)^2 - (ccX - x3)^2 - (ccY - y3)^2\]

Adding them:

\[0 = 2(ccX - x1)^2 + 2(ccY - y1)^2 - (ccX - x2)^2 - (ccY - y2)^2 - (ccX - x3)^2 - (ccY - y3)^2\]

Substitute:

\[0 = 2(ccX - (Ax + Adx \cdot i))^2 + 2(ccY - (Ay + Ady \cdot i))^2\] \[- (ccX - (Bx + Bdx \cdot j))^2 - (ccY - (By + Bdy \cdot j))^2\] \[- (ccX - (Cx + Cdx \cdot k))^2 - (ccY - (Cy + Cdy \cdot k))^2\]

Expand:

\[0 = 2 \cdot {ccX}^2 - 4 \cdot ccX \cdot Ax - 4 \cdot ccX \cdot Adx \cdot i + 2\cdot {Ax}^2 + 4 \cdot Ax \cdot Adx \cdot i + 2{(Adx)}^2 i^2\] \[+ 2 \cdot {ccY}^2 - 4 \cdot ccY \cdot Ay - 4 \cdot ccY \cdot Ady \cdot i + 2 \cdot {Ay}^2 + 4 \cdot Ay \cdot Ady \cdot i + 2{(Ady)}^2 i^2\] \[- \ {ccX}^2 + 2 \cdot ccX \cdot Bx + 2 \cdot ccX \cdot Bdx \cdot j - {Bx}^2 - 2 \cdot Bx \cdot Bdx \cdot j - {(Bdx)}^2 j^2\] \[- \ {ccY}^2 + 2 \cdot ccY \cdot By + 2 \cdot ccY \cdot Bdy \cdot j - {By}^2 - 2 \cdot By \cdot Bdy \cdot j - {(Bdy)}^2 j^2\] \[- \ {ccX}^2 + 2 \cdot ccX \cdot Cx + 2 \cdot ccX \cdot Cdx \cdot k - {Cx}^2 - 2 \cdot Cx \cdot Cdx \cdot k - {(Cdx)}^2 k^2\] \[- \ {ccY}^2 + 2 \cdot ccY \cdot Cy + 2 \cdot ccY \cdot Cdy \cdot k - {Cy}^2 - 2 \cdot Cy \cdot Cdy \cdot k - {(Cdy)}^2 k^2\]

Collect unknown terms:

\[0 = i^2 \cdot (2{(Adx)}^2 + 2{(Ady)}^2)\] \[+ \ j^2 \cdot (-{(Bdx)}^2 - {(Bdy)}^2)\] \[+ \ k^2 \cdot (-{(Cdx)}^2 - {(Cdy)}^2)\] \[+ \ i \cdot (-4 \cdot ccX \cdot Adx + 4 \cdot Ax \cdot Adx - 4 \cdot ccY \cdot Ady + 4 \cdot Ay \cdot Ady)\] \[+ \ j \cdot (2 \cdot ccX \cdot Bdx - 2 \cdot Bx \cdot Bdx + 2 \cdot ccY \cdot Bdy - 2 \cdot By \cdot Bdy)\] \[+ \ k \cdot (2 \cdot ccX \cdot Cdx - 2 \cdot Cx \cdot Cdx + 2 \cdot ccY \cdot Cdy - 2 \cdot Cy \cdot Cdy)\] \[- \ 4 \cdot ccX \cdot Ax + 2 \cdot {Ax}^2 - 4 \cdot ccY \cdot Ay + 2 \cdot {Ay}^2\] \[+ \ 2 \cdot ccX \cdot Bx - {Bx}^2 + 2 \cdot ccY \cdot By - {By}^2\] \[+ \ 2 \cdot ccX \cdot Cx - {Cx}^2 + 2 \cdot ccY \cdot Cy - {Cy}^2\]

\[0 = i^2 \cdot t_1 + j^2 \cdot t_2 + k^2 \cdot t_3 + i \cdot t_4 + j \cdot t_5 + k \cdot t_6 + t_7\]

Finally we can write as vectors for LLL:

\[i^2 \begin{bmatrix}t_1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0\end{bmatrix} + j^2 \begin{bmatrix}t_2 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0\end{bmatrix} + k^2 \begin{bmatrix}t_3 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0\end{bmatrix} + i \begin{bmatrix}t_4 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0\end{bmatrix} + j \begin{bmatrix}t_5 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0\end{bmatrix} + k \begin{bmatrix}t_6 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1\end{bmatrix} + \begin{bmatrix}t_7 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0\end{bmatrix} = \begin{bmatrix}0 \\ i^2 \\ j^2 \\ k^2 \\ i \\ j \\ k\end{bmatrix}\]

Demo:

from sympy import Point, Triangle

def r():
    return randint(0, 2**1000)

i, j, k = [randint(0, 2**32) for _ in range(3)]
print(i, j, k)

Ax, Bx, Cx    = r(), r(), r()
Ay, By, Cy    = r(), r(), r()
Adx, Bdx, Cdx = r(), r(), r()
Ady, Bdy, Cdy = r(), r(), r()

x1, y1 = Ax + Adx*i, Ay + Ady*i
x2, y2 = Bx + Bdx*j, By + Bdy*j
x3, y3 = Cx + Cdx*k, Cy + Cdy*k

triangle = Triangle(Point(x1, y1), 
                    Point(x2, y2), 
                    Point(x3, y3)) 

ccX, ccY = triangle.circumcenter

assert (ccX - x1)**2 + (ccY - y1)**2 == (ccX - x2)**2 + (ccY - y2)**2 == (ccX - x3)**2 + (ccY - y3)**2
assert 0 == (ccX - x1)**2 + (ccY - y1)**2 - (ccX - x2)**2 - (ccY - y2)**2 
assert 0 == (ccX - x1)**2 + (ccY - y1)**2 - (ccX - x3)**2 - (ccY - y3)**2
assert 0 == 2*(ccX-x1)**2 + 2*(ccY-y1)**2 - (ccX-x2)**2 - (ccY-y2)**2 - (ccX-x3)**2 - (ccY-y3)**2
assert 0 == 2*(ccX-(Ax+Adx*i))**2 + 2*(ccY-(Ay+Ady*i))**2 - (ccX-(Bx+Bdx*j))**2 - (ccY-(By+Bdy*j))**2 - (ccX-(Cx+Cdx*k))**2 - (ccY-(Cy+Cdy*k))**2

assert 0 == 2*ccX**2 - 4*ccX*Ax - 4*ccX*Adx*i + 2*Ax**2 + 4*Ax*Adx*i + 2*Adx**2*i**2 + \
            2*ccY**2 - 4*ccY*Ay - 4*ccY*Ady*i + 2*Ay**2 + 4*Ay*Ady*i + 2*Ady**2*i**2 - \
              ccX**2 + 2*ccX*Bx + 2*ccX*Bdx*j -   Bx**2 - 2*Bx*Bdx*j -   Bdx**2*j**2 - \
              ccY**2 + 2*ccY*By + 2*ccY*Bdy*j -   By**2 - 2*By*Bdy*j -   Bdy**2*j**2 - \
              ccX**2 + 2*ccX*Cx + 2*ccX*Cdx*k -   Cx**2 - 2*Cx*Cdx*k -   Cdx**2*k**2 - \
              ccY**2 + 2*ccY*Cy + 2*ccY*Cdy*k -   Cy**2 - 2*Cy*Cdy*k -   Cdy**2*k**2 

assert 0 == i**2 * (2*Adx**2 + 2*Ady**2) + \
            j**2 * (-Bdx**2 - Bdy**2) + \
            k**2 * (-Cdx**2 - Cdy**2) + \
            i    * (-4*ccX*Adx + 4*Ax*Adx - 4*ccY*Ady + 4*Ay*Ady) + \
            j    * (2*ccX*Bdx - 2*Bx*Bdx + 2*ccY*Bdy - 2*By*Bdy) + \
            k    * (2*ccX*Cdx - 2*Cx*Cdx + 2*ccY*Cdy - 2*Cy*Cdy) + \
            2*ccX**2 - 4*ccX*Ax + 2*Ax**2 + 2*ccY**2 - 4*ccY*Ay + 2*Ay**2 + \
            -ccX**2 + 2*ccX*Bx - Bx**2 - ccY**2 + 2*ccY*By - By**2 + \
            -ccX**2 + 2*ccX*Cx - Cx**2 - ccY**2 + 2*ccY*Cy - Cy**2


assert 0 == i**2 * (2*Adx**2 + 2*Ady**2) + \
            j**2 * (-Bdx**2 - Bdy**2) + \
            k**2 * (-Cdx**2 - Cdy**2) + \
            i    * (-4*ccX*Adx + 4*Ax*Adx - 4*ccY*Ady + 4*Ay*Ady) + \
            j    * (2*ccX*Bdx - 2*Bx*Bdx + 2*ccY*Bdy - 2*By*Bdy) + \
            k    * (2*ccX*Cdx - 2*Cx*Cdx + 2*ccY*Cdy - 2*Cy*Cdy) + \
            - 4*ccX*Ax + 2*Ax**2 - 4*ccY*Ay + 2*Ay**2 + \
            + 2*ccX*Bx -   Bx**2 + 2*ccY*By -   By**2 + \
            + 2*ccX*Cx -   Cx**2 + 2*ccY*Cy -   Cy**2

t1 = 2*Adx**2 + 2*Ady**2
t2 = -Bdx**2 - Bdy**2
t3 = -Cdx**2 - Cdy**2
t4 = -4*ccX*Adx + 4*Ax*Adx - 4*ccY*Ady + 4*Ay*Ady
t5 = 2*ccX*Bdx - 2*Bx*Bdx + 2*ccY*Bdy - 2*By*Bdy
t6 = 2*ccX*Cdx - 2*Cx*Cdx + 2*ccY*Cdy - 2*Cy*Cdy
t7 = - 4*ccX*Ax + 2*Ax**2 - 4*ccY*Ay + 2*Ay**2 + 2*ccX*Bx - Bx**2 + \
        2*ccY*By - By**2 + 2*ccX*Cx - Cx**2 + 2*ccY*Cy - Cy**2

assert 0 == i**2*t1 + j**2*t2 + k**2*t3 + i*t4 + j*t5 + k*t6 + t7

M = Matrix([
    [t1, 1, 0, 0, 0, 0, 0],
    [t2, 0, 1, 0, 0, 0, 0],
    [t3, 0, 0, 1, 0, 0, 0],
    [t4, 0, 0, 0, 1, 0, 0],
    [t5, 0, 0, 0, 0, 1, 0],
    [t6, 0, 0, 0, 0, 0, 1],
    [t7, 0, 0, 0, 0, 0, 0],
])

print(M.LLL()[0][-3:])

from sympy import Float, Triangle, Point
import secrets

class RandomLine:
    def __init__(self):
        self.x = randFloat()
        self.y = randFloat()
        self.dx = randFloat()
        self.dy = randFloat()

    def __getitem__(self, i):
        return Point(self.x + self.dx * i, self.y + self.dy * i, evaluate=False)

    def get(self):
        return self.x, self.y, self.dx, self.dy

def randFloat():
    # return a random float between -1 and 1
    PRECISION = 1337
    return -1 + 2 * Float(secrets.randbits(PRECISION), PRECISION) / (1 << PRECISION)

A = RandomLine()
B = RandomLine()
C = RandomLine()
i, j, k = [randint(0, 2**32) for _ in range(3)]
print(i, j, k)
triangle = Triangle(A[i], B[j], C[k])

Ax, Ay, Adx, Ady = A.get()
Bx, By, Bdx, Bdy = B.get()
Cx, Cy, Cdx, Cdy = C.get()
ccX, ccY = triangle.circumcenter

t1 = 2*Adx**2 + 2*Ady**2
t2 = -Bdx**2 - Bdy**2
t3 = -Cdx**2 - Cdy**2
t4 = -4*ccX*Adx + 4*Ax*Adx - 4*ccY*Ady + 4*Ay*Ady
t5 = 2*ccX*Bdx - 2*Bx*Bdx + 2*ccY*Bdy - 2*By*Bdy
t6 = 2*ccX*Cdx - 2*Cx*Cdx + 2*ccY*Cdy - 2*Cy*Cdy
t7 = - 4*ccX*Ax + 2*Ax**2 - 4*ccY*Ay + 2*Ay**2 + 2*ccX*Bx - Bx**2 + \
        2*ccY*By - By**2 + 2*ccX*Cx - Cx**2 + 2*ccY*Cy - Cy**2

M = Matrix([
    [t1, 1, 0, 0, 0, 0, 0],
    [t2, 0, 1, 0, 0, 0, 0],
    [t3, 0, 0, 1, 0, 0, 0],
    [t4, 0, 0, 0, 1, 0, 0],
    [t5, 0, 0, 0, 0, 1, 0],
    [t6, 0, 0, 0, 0, 0, 1],
    [t7, 0, 0, 0, 0, 0, 0],
])

# resize
for i in range(M.nrows()):
    M[i, 0] = int(M[i, 0] * 10**1337)

print(M.change_ring(ZZ).LLL()[0][-3:])

ETA - leaving it as two equations rather than combining them to one is an alternative:

from sympy import Point, Triangle

def r():
    return randint(0, 2**1000)

i, j, k = [randint(0, 2**32) for _ in range(3)]
print(i, j, k)

Ax, Bx, Cx    = r(), r(), r()
Ay, By, Cy    = r(), r(), r()
Adx, Bdx, Cdx = r(), r(), r()
Ady, Bdy, Cdy = r(), r(), r()

x1, y1 = Ax + Adx*i, Ay + Ady*i
x2, y2 = Bx + Bdx*j, By + Bdy*j
x3, y3 = Cx + Cdx*k, Cy + Cdy*k

triangle = Triangle(Point(x1, y1), 
                    Point(x2, y2), 
                    Point(x3, y3)) 

ccX, ccY = triangle.circumcenter

assert (ccX - x1)**2 + (ccY - y1)**2 == (ccX - x2)**2 + (ccY - y2)**2 == (ccX - x3)**2 + (ccY - y3)**2
assert 0 == (ccX - x1)**2 + (ccY - y1)**2 - (ccX - x2)**2 - (ccY - y2)**2 
assert 0 == (ccX - x1)**2 + (ccY - y1)**2 - (ccX - x3)**2 - (ccY - y3)**2

assert 0 == (ccX-(Ax+Adx*i))**2 + (ccY-(Ay+Ady*i))**2 - (ccX-(Bx+Bdx*j))**2 - (ccY-(By+Bdy*j))**2 
assert 0 == (ccX-(Ax+Adx*i))**2 + (ccY-(Ay+Ady*i))**2 - (ccX-(Cx+Cdx*k))**2 - (ccY-(Cy+Cdy*k))**2

assert 0 == ccX**2 - 2*ccX*Ax - 2*ccX*Adx*i + Ax**2 + 2*Ax*Adx*i + Adx**2*i**2 + \
            ccY**2 - 2*ccY*Ay - 2*ccY*Ady*i + Ay**2 + 2*Ay*Ady*i + Ady**2*i**2 - \
            ccX**2 + 2*ccX*Bx + 2*ccX*Bdx*j - Bx**2 - 2*Bx*Bdx*j - Bdx**2*j**2 - \
            ccY**2 + 2*ccY*By + 2*ccY*Bdy*j - By**2 - 2*By*Bdy*j - Bdy**2*j**2
assert 0 == ccX**2 - 2*ccX*Ax - 2*ccX*Adx*i + Ax**2 + 2*Ax*Adx*i + Adx**2*i**2 + \
            ccY**2 - 2*ccY*Ay - 2*ccY*Ady*i + Ay**2 + 2*Ay*Ady*i + Ady**2*i**2 - \
            ccX**2 + 2*ccX*Cx + 2*ccX*Cdx*k - Cx**2 - 2*Cx*Cdx*k - Cdx**2*k**2 - \
            ccY**2 + 2*ccY*Cy + 2*ccY*Cdy*k - Cy**2 - 2*Cy*Cdy*k - Cdy**2*k**2

assert 0 == i**2 * (Adx**2 + Ady**2) + \
            j**2 * (-Bdx**2 - Bdy**2) + \
            i    * ( 2*Ax*Adx - 2*ccX*Adx + 2*Ay*Ady - 2*ccY*Ady) + \
            j    * (-2*Bx*Bdx + 2*ccX*Bdx - 2*By*Bdy + 2*ccY*Bdy) + \
            Ax**2 + Ay**2 - Bx**2 - By**2 - 2*ccX*Ax - 2*ccY*Ay + 2*ccX*Bx + 2*ccY*By
assert 0 == i**2 * (Adx**2 + Ady**2) + \
            k**2 * (-Cdx**2 - Cdy**2) + \
            i    * ( 2*Ax*Adx - 2*ccX*Adx + 2*Ay*Ady - 2*ccY*Ady) + \
            k    * (-2*Cx*Cdx + 2*ccX*Cdx - 2*Cy*Cdy + 2*ccY*Cdy) + \
            Ax**2 + Ay**2 - Cx**2 - Cy**2 - 2*ccX*Ax - 2*ccY*Ay + 2*ccX*Cx + 2*ccY*Cy

u1 = Adx**2 + Ady**2
u2 = -Bdx**2 - Bdy**2
u3 = 2*(Ax*Adx-ccX*Adx+Ay*Ady-ccY*Ady)
u4 = 2*(-Bx*Bdx+ccX*Bdx-By*Bdy+ccY*Bdy)
u5 = Ax**2 + Ay**2 - Bx**2 - By**2 + 2*(ccX*Bx+ccY*By-ccX*Ax-ccY*Ay)
u6 = -Cdx**2 - Cdy**2
u7 = 2*(-Cx*Cdx+ccX*Cdx-Cy*Cdy+ccY*Cdy)
u8 = Ax**2 + Ay**2 - Cx**2 - Cy**2 + 2*(ccX*Cx+ccY*Cy-ccX*Ax-ccY*Ay)

assert 0 == i**2*u1 + j**2*u2 + i*u3 + j*u4 + u5
assert 0 == i**2*u1 + k**2*u6 + i*u3 + k*u7 + u8

M = Matrix([
    [u1, u1, 1, 0, 0, 0, 0, 0],
    [u2,  0, 0, 1, 0, 0, 0, 0],
    [ 0, u6, 0, 0, 1, 0, 0, 0],
    [u3, u3, 0, 0, 0, 1, 0, 0],
    [u4,  0, 0, 0, 0, 0, 1, 0],
    [ 0, u7, 0, 0, 0, 0, 0, 1],
    [u5, u8, 0, 0, 0, 0, 0, 0],
])

print(M.LLL()[0][-3:])

Part 3 - Incenter:

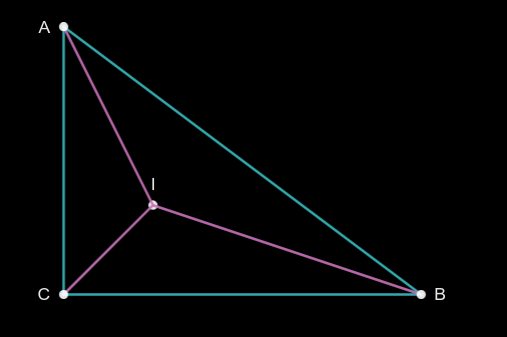
Pick some equal angles, eg \(\angle CBI = \angle ABI\)

Then we have a choice of formulas to use for the angle between two vectors:

\[\cos \theta = \frac{\vec{v} \cdot \vec{w}}{||\vec{v}|| \ ||\vec{w}||} \ , \ \sin \theta = \frac{||\vec{v} \times \vec{w}||}{||\vec{v}|| \ ||\vec{w}||} \ , \ \tan \theta = \frac{||\vec{v} \times \vec{w}||}{\vec{v} \cdot \vec{w}}\] \[BA =\pmatrix{x_1-x_2 \\ y_1-y_2}, \ BC =\pmatrix{x_3-x_2 \\ y_3-y_2}, \ BI =\pmatrix{I_x-x_2 \\ I_y-y_2}\]

Trying cos doesn’t work:

\[\cos (\angle CBI) = \cos (\angle ABI)\] \[\frac{BC \cdot BI}{||BC|| \ ||BI||} = \frac{BA \cdot BI}{||BA|| \ ||BI||}\] \[\frac{BC \cdot BI}{||BC||} = \frac{BA \cdot BI}{||BA||}\] \[\frac{(x_3-x_2)(I_x-x_2) + (y_3-y_2)(I_y-y_2)}{\sqrt{(x_3-x_2)^2 + (y_3-y_2)^2}} = \frac{(x_1-x_2)(I_x-x_2) + (y_1-y_2)(I_y-y_2)}{\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}}\] \[\frac{((x_3-x_2)(I_x-x_2) + (y_3-y_2)(I_y-y_2))^2}{(x_3-x_2)^2 + (y_3-y_2)^2} = \frac{((x_1-x_2)(I_x-x_2) + (y_1-y_2)(I_y-y_2))^2}{(x_1-x_2)^2 + (y_1-y_2)^2}\]

lhs = ((x3-x2)*(Ix-x2)+(y3-y2)*(Iy-y2))^2 * ((x1-x2)^2 + (y1-y2)^2)
rhs = ((x1-x2)*(Ix-x2)+(y1-y2)*(Iy-y2))^2 * ((x3-x2)^2 + (y3-y2)^2)

Trying sin doesn’t work:

\[\sin (\angle CBI) = \sin (\angle ABI)\] \[\frac{||BC \times BI||}{||BC|| \ ||BI||} = \frac{||BA \times BI||}{||BA|| \ ||BI||}\] \[\frac{||BC \times BI||}{||BC||} = \frac{||BA \times BI||}{||BA||}\] \[\frac{(x_3-x_2)(I_y-y_2) - (y_3-y_2)(I_x-x_2)}{\sqrt{(x_3-x_2)^2 + (y_3-y_2)^2}} = \frac{(x_1-x_2)(I_y-y_2) - (y_1-y_2)(I_x-x_2)}{\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}}\] \[\frac{((x_3-x_2)(I_y-y_2) - (y_3-y_2)(I_x-x_2))^2}{(x_3-x_2)^2 + (y_3-y_2)^2} = \frac{((x_1-x_2)(I_y-y_2) - (y_1-y_2)(I_x-x_2))^2}{(x_1-x_2)^2 + (y_1-y_2)^2}\]

lhs = ((x3-x2)*(Iy-y2)-(y3-y2)*(Ix-x2))^2 * ((x1-x2)^2 + (y1-y2)^2)
rhs = ((x1-x2)*(Iy-y2)-(y1-y2)*(Ix-x2))^2 * ((x3-x2)^2 + (y3-y2)^2)

But trying tan works! Maybe because there’s no square roots to deal with?:

\[\tan (\angle CBI) = \tan (\angle ABI)\] \[\frac{||BC \times BI||}{BC \cdot BI} = \frac{||BI \times BA||}{BA \cdot BI}\] \[\frac{(x_3-x_2)(I_y-y_2) - (y_3-y_2)(I_x-x_2)}{(x_3-x_2)(I_x-x_2) + (y_3-y_2)(I_y-y_2)} = \frac{(y_1-y_2)(I_x-x_2) - (x_1-x_2)(I_y-y_2)}{(x_1-x_2)(I_x-x_2) + (y_1-y_2)(I_y-y_2)}\]

from sympy import Float, Triangle, Point
import secrets
from tqdm import tqdm

class RandomLine:
    def __init__(self):
        self.x = randFloat()
        self.y = randFloat()
        self.dx = randFloat()
        self.dy = randFloat()

    def __getitem__(self, i):
        return Point(self.x + self.dx * i, self.y + self.dy * i, evaluate=False)

    def get(self):
        return self.x, self.y, self.dx, self.dy

def randFloat():
    # return a random float between -1 and 1
    PRECISION = 1337
    return -1 + 2 * Float(secrets.randbits(PRECISION), PRECISION) / (1 << PRECISION)

A = RandomLine()
B = RandomLine()
C = RandomLine()
Ax, Ay, Adx, Ady = A.get()
Bx, By, Bdx, Bdy = B.get()
Cx, Cy, Cdx, Cdy = C.get()

i_, j_, k_ = [randint(0, 2**32) for _ in range(3)]
print(i_, j_, k_)
triangle = Triangle(A[i_], B[j_], C[k_])
Ix, Iy = triangle.incenter

def solve(equation):
    coeffs = equation.polynomial(QQ).coefficients()
    M = Matrix(coeffs).transpose()
    n = M.nrows()
    M = M.augment(identity_matrix(n))
    M[-1, -1] = 0

    # resize
    for i in range(n):
        M[i, 0] = M[i, 0] * 10**1337

    M = M.LLL()
    print(M[0][-4:])

i, j, k = var('i'), var('j'), var('k')
x1, y1 = Ax + Adx*i, Ay + Ady*i
x2, y2 = Bx + Bdx*j, By + Bdy*j
x3, y3 = Cx + Cdx*k, Cy + Cdy*k

lhs = ((x3-x2)*(Iy-y2)-(y3-y2)*(Ix-x2)) * ((x1-x2)*(Ix-x2)+(y1-y2)*(Iy-y2))
rhs = ((y1-y2)*(Ix-x2)-(x1-x2)*(Iy-y2)) * ((x3-x2)*(Ix-x2)+(y3-y2)*(Iy-y2))
equation = lhs - rhs

print(int(lhs(i=i_, j=j_, k=k_)) == int(rhs(i=i_, j=j_, k=k_)))
solve(equation)